Question

1. A total of three freshmen, five sophomores, 3 juniors and 4 seniors are eligible for a $3000 scholarship, a $2000 scholarship and a $1000 scholarship. In how many different ways can these scholarships be awarded if at least two of them must go to senior

Answer 1

So those scholarships can be awarded in 13*12 = 156 different ways ensuring that at least two of them go to seniors.

Explanation:

In this problem, there are three scolarships.

The first step to solve this question is ensuring that two seniors receive their scolarships.

There are 4 seniors, and we must guarantee two scolarships to them. If senior A receives the first scolarship and senior B the second, or A receives the second and B the first, it is the same thing, so the order does not interfere with the problem. It means it is a combination problem.

------------------------------

The formula for the number of possible combinations of r objects from a set of n objects is:

`C(n,r) = (n!)/(r!(n-r)!)`

------------------------------

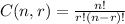
So, for the senior scolarships, we have combinations of two(scolarships) objects from a set of four(seniors) objects: So

`C(4,2) = (4!)/(4!(4-2)!) = 12`

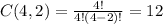
There are 12 ways to ensure two of those scolarships to those seniors.

The are 13 students vying for the last scolarship(hree freshmen, five sophomores, 3 juniors and two seniors that didn't get the first two).

So those scholarships can be awarded in 13*12 = 156 different ways ensuring that at least two of them go to seniors.