Question

Because weightlessness in outer space causes astronauts to lose bone mass, at the end of each month, an astronaut has two percent less bone mass than at the beginning of that month. If Lori has a 6-month mission on the International Space Station, what percentage of her bone mass will remain when she returns to Earth

Answer 1

There will be 88.6% of her bone mass remaining when she returns to earth.

Explanation:

According to the problem, the astronaut will have 2% less bone mass than at the beginning of that month. So let's say
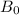`B_(0)` is her original bone mass. In that case, her bone mass after the first month will be:

`B_(1)=B_(0)(0.98)`

on the second month, her bone mass will be:

`B_(2)=B_(1)(0.98)=B_(0)(0.98)(0.98)=B_(0)(0.98)^(2)`

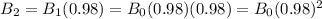
on the third month, her bone mass will be:

`B_(3)=B_(2)(0.98)=B_(0)(0.98)(0.98)(098)=B_(0)(0.98)^(3)`

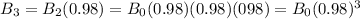
and so on, we can see a pattern here. The formula for her remaining bone mass can be generally written like this:

`B_(n)=B_(0)(0.98)^(n)`

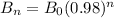
where n is the number of months, so after 6 months, her remaining bone mass will be:

`B_(6)=B_(0)(0.98)^(6)=0.886B_(0)`

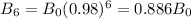
that 0.886 gives us the percentage as a decimal number. When turned into a percentage we get that:

There will be 88.6% of her bone mass remaining after 6 months.