Answer:
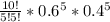
Explanation:
In order to be in the starting point after 10 steps the man must take five steps backward and five steps forward, no matter in which order.
For instance the sequence B-B-B-B-B-F-F-F-F-F yields the same the result of the sequence B-F-B-F-B-F-B-F-B-F. For that reason we can count the ways the man ends up at his starting point. We perform a pemutation with repeating elements and then we multiply that by the probability of taking 5 steps forward (0.6^5) and by the probability of taking 5 steps backward (0.4^5)