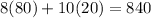Question

A firm buys two inputs, labor L and capital K, the total amount of which cannot exceed 100. The wage is $8, and the rental rate is $10. The firm can at most spend $840 on the two inputs.

a. Write the two equations:

Input limit: K + L = 100
Budget limit: 8 x K + 10 x L = 840

b. What are the quantities of two inputs the firm must buy in order to produce a maximum output, given input and budget constraints?

L=
K=

Answer 1

L= 80

K= 20

Step-by-step explanation:

The guy who solved this question he perfectly explained but he did mistake on putting a correct answer at L=20 and K=80. Just reverse the L and K mistake.

Answer 2

a.

Input limit:
`K+L=100`

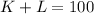
Budget limit:
`8K+10L=840`

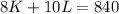
b.

L=20

K=80

Step-by-step explanation:

Ok, you save me a little bit of work and resolved the point a.

Indeed, the equations for Input limit and Budget limit are the ones you put in the question.

Now I will show you how to find the quantities of the two inputs in order to have a maximum output taking into account the input limit and the budget limit:

First, we need to put our equations in function of one of the variables, lets do it with L (Labor):

Input limit:

`K+L=100`

`L=100-K`

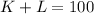
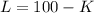
Budget Limit:

`8K+10L=840`

`L=(840-8K)/(10)`

`L=84-0.8K`

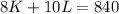
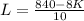
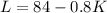
Now we match the 2 equations and find the value of K

L=L

`100-K=84-0.8K`

`100-84=-0.8K + K`

`0.2K=16`

`K=(16)/(0.2)`

`K=80`

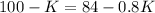
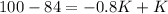
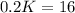
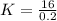
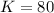
Now that we have the optimum K we replace in any of the two equations to find the optimum L

`L=100-80=20`

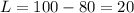
And then we replace in the Input limit and Budget limit equations to verify:

Input limit:

`80 + 20 = 100`

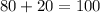
Budget Limit:

`8(80)+10(20)=840`