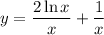Question

Differential Equations: Solve the initial value problem

x2y' - xy = 2

y(1) = 1

Answer 1

`y=\displaystyle(2\ln x)/(x)+(1)/(x)`

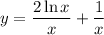
Step-by-step explanation:

Divide both sides of the equation by
`x^2`:

`\displaystyle y'-(1)/(x)y=(2)/(x^2)`

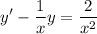
Find the integrating factor:

`u=e^{\int(1)/(x)}=e^(\ln x)=x`

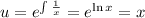
Multiply the equation by the integrating factor:

`\displaystyle xy'-y=(2)/(x)`

The left side is the derivative of (xy), therefore we can write the equation as:

`\displaystyle(d(xy))/(dx)=(2)/(x)`

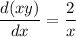
That is a separable equation. We separate and integrate:

`\displaystyle\int d(xy)=\int(2)/(x)dx`

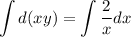
We get:

`xy=2\ln x + C`

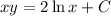
Then plug the initial value y(1)=1, which means to plug x=1 and y=1:

`1(1)=2\ln 1 + C\to 1= C`

Therefore, the solution once we plug C=1 becomes:

`xy=2\ln x+1`

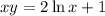
Then solving for y by dividing both sides by x, we get:

`y=\displaystyle(2\ln x)/(x)+(1)/(x)`