Answer:
The width of the walkway is 4 feet.
Explanation:
The garden and a walkway around its perimeter have an area of 460 square feet.
The length of the garden = 15 feet
The width of the garden = 12 feet
Assuming that walkway is of uniform width, we can solve the following equation.
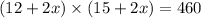
Expanding this we get;

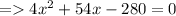
We will solve this using quadratic equation formula:
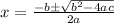
Here a = 4 , b = 54 , c = -280
We get the roots as x = 4 and x =
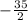
Neglecting the negative value, we will take x = 4 feet.
Hence, the width of the walkway is 4 feet.