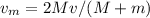Question

Show that in a collision between a heavy particle and an electron the highest speed the electron can receive is 2Mv/(M+mo), where v is the speed of the heavy particle and M and mo are the rest masses of the heavy particle and the electron. Assume non-relativistic particles.

Answer 1

`v_(m) =2Mv/(M+m)`

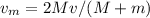
Step-by-step explanation:

1. We have to apply the momentums conservation principle. The momentum before the collision is the same at the momentum after the collision.
2. If the electron receives the highest speed possible, so the energy is conserved during the collision.

before the collision, the velocity of the heavy particle is v:

`p=Mv`

`E=1/2Mv^2`

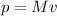
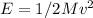
After the collision :

`p=mv_(m)+Mv_(M)`

`E=1/2mv_(m) ^(2) +1/2Mv_(M) ^(2)`

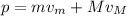
So:

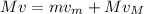`Mv=mv_(m)+Mv_(M)` (1)

`1/2Mv^(2)=1/2mv_(m) ^(2) +1/2Mv_(M) ^(2)` ⇒
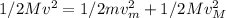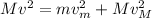`Mv^(2)=mv_(m) ^(2) +Mv_(M) ^(2)` (2)

in the first equation:

`v_(M) ^(2)=(1/M*(Mv-mv_(m)))^(2)`

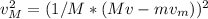
if we replace
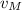`v_(M)` in the equation (2):

`Mv^(2)=mv_(m) ^(2)+1/M*(Mv-mv_(m))^(2)`

`M^(2)*v^(2)=mMv_(m) ^(2)+M^(2)*v^(2)-2Mmvv_(m)+m^(2)v_(m)^(2)`

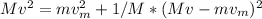
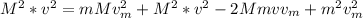
so:

`0=Mv_(m) ^(2)-2Mvv_(m)+mv_(m)^(2)`

`2Mvv_(m)=Mv_(m) ^(2)+mv_(m)^(2)=v_(m) ^(2)(M+m)`

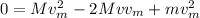
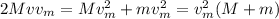
Finally:

`v_(m) =2Mv/(M+m)`