Answer:
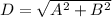 and
and
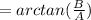
Step-by-step explanation:
Hi! Since the notation is a little bit messed up, I am going to suppose that
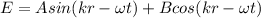 --- (1)
--- (1)
and :
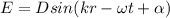 --- (2)
--- (2)
Here we are going to use a trigonometric identity of the sine of the sum of two angles, namely:
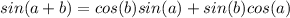 --- (3)
--- (3)
Lets set:
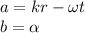
So now (2) becomes:
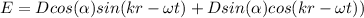 --- (4)
--- (4)
Now (1) and (4) must be equal, and in particular we must have the following identities:
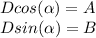 --- (5)
--- (5)
If we square these two identities and sum them we got:
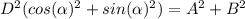
And since:
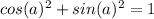
We got the first solution:
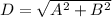
For the second part we must divide the identies (5)
We got:
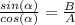
And since:
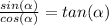
We use the inverse of the tan function:
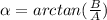
Greetings!