Answer:
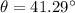
Step-by-step explanation:
Given that,
Number of lines,
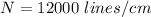
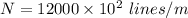
Wavelength,
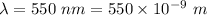
We need to find the angle for the first order maximum, n = 1
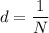
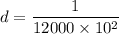
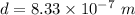
Using the grating equation as :
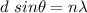
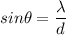
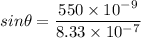
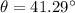
So, the angle for the first order maximum is 41.29 degrees. Hence, this is the required solution.