Answer:

Step-by-step explanation:
The electric field of a plane standing electromagnetic wave in a vacuum is given by :
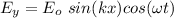
We need to find the corresponding expression for the magnetic field. According to equation of Maxwell's :
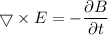
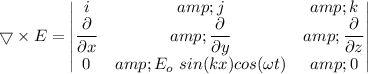
![\bigtriangledown * E=k[E_ok\ cos(kx)cos(\omega t)]=-(\partial B)/(\partial t)](https://img.qammunity.org/2020/formulas/physics/college/tufyhd8cjtymoud3e8x3va2k9jfkozcrlp.png)
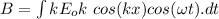
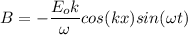
Since,
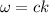

So, the corresponding expression for the magnetic field is
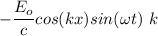 . Hence, this is the required solution.
. Hence, this is the required solution.