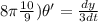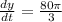Answer:
The beam of light is moving at the peed of:
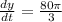 km/min
km/min
Given:
Distance from the isalnd, d = 3 km
No. of revolutions per minute, n = 4
Solution:
Angular velocity,
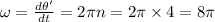 (1)
(1)
Now, in the right angle in the given fig.:
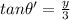
Now, differentiating both the sides w.r.t t:
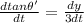
Applying chain rule:
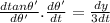
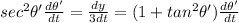
Now, using
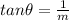 and y = 1 in the above eqn, we get:
and y = 1 in the above eqn, we get:
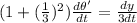
Also, using eqn (1),