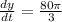Question

A lighthouse is located on a small island, 3 km away from the nearest point on a straight shoreline, and its light makes four revolutions per minute. How fast is the beam of light moving along the shoreline when it is 1 km from ?

Answer 1

The beam of light is moving at the peed of:

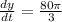`(dy)/(dt) = (80\pi)/(3)` km/min

Given:

Distance from the isalnd, d = 3 km

No. of revolutions per minute, n = 4

Solution:

Angular velocity,
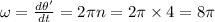`\omega = (d\theta')/(dt) = 2\pi n = 2\pi * 4 = 8\pi` (1)

Now, in the right angle in the given fig.:

`tan\theta' = (y)/(3)`

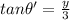
Now, differentiating both the sides w.r.t t:

`(dtan\theta')/(dt) = (dy)/(3dt)`

Applying chain rule:

`(dtan\theta')/(d\theta').(d\theta')/(dt) = (dy)/(3dt)`

`sec^(2)\theta'(d\theta')/(dt) = (dy)/(3dt) = (1 + tan^(2)\theta')(d\theta')/(dt)`

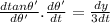
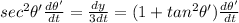
Now, using
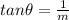`tan\theta = (1)/(m)` and y = 1 in the above eqn, we get:

`(1 + ((1)/(3))^(2))(d\theta')/(dt) = (dy)/(3dt)`

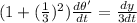
Also, using eqn (1),

`8\pi(10)/(9))\theta' = (dy)/(3dt)`

`(dy)/(dt) = (80\pi)/(3)`