Question

A proton is projected perpendicularly into a magnetic field that has a magnitude of 0.50 T. The field is then adjusted so that an electron will follow a circular path of the same radius when it is projected perpendicularly into the field with the same velocity that the proton had. What is the magnitude of the field used for the electron?

Answer 1

2.73 x 10^-4 T

Step-by-step explanation:

The relation between the radius of circular path and the velocity is given by

`r=(mv)/(Bq)`

Where, m be the mass of charged particle and q be the charge on the charged particle.

For proton:

mass of proton = mp = 1.67 x 10^-27 kg

charge of proton = q = 1.6 x 10^-19 C

magnetic field strength, B = 0.50 T

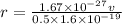`r=(1.67* 10^(-27)v)/(0.5 * 1.6 * 10^(-19))` ..... (1)

For electron:

mass of electron = me = 9.1 x 10^-31 kg

charge of electron = q = 1.6 x 10^-19 C

let the strength of magnetic field is B.

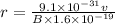`r=(9.1* 10^(-31)v)/(B * 1.6 * 10^(-19))` ..... (2)

As the radius and the velocity is same for both the particles, so by comparing equation (1) and equation (2), we get

`(1.67* 10^(-27)v)/(0.5 * 1.6 * 10^(-19)) = (9.1* 10^(-31)v)/(B * 1.6 * 10^(-19))`

`B = (9.1*10^(-31)*0.5)/(1.67*10^(-27))`

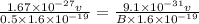
B = 2.73 x 10^-4 T

Thus, the magnetic field required for electron is 2.73 x 10^-4 T.

Answer 2

`B_e = 2.72 * 10^(-4) T`

Step-by-step explanation:

As we know that when charge particle is projected in perpendicular magnetic field then the radius of the charge particle is given as

`F = qvB`

`(mv^2)/(r) = qvB`

now we have

`r = (mv)/(qB)`

since here radius of proton and electron will be same

so we will have

`r_e = r_p`

`(m_e v)/(q_e B_e) = (m_p v)/(q_p B_p)`

so we have

`B_e = (B_p m_e)/(m_p)`

given that

`B_p = 0.50 T`

`m_e = 9.11 * 10^(-31) kg`

`m_p = 1.67 * 10^(-27) kg`

so we have

`B_e = (0.50(9.11* 10^(-31)))/(1.67* 10^(-27))`

`B_e = 2.72 * 10^(-4) T`