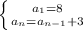Question

What is the recursive rule for a n=3n+5

Answer 1

i believe the answer is -2n=5

Step-by-step explanation:you subtract the 3n with the n and -2n cant go into 5

Answer 2

`\left \{ {{a_(1) =8} \atop {a_(n) =a_(n-1) +3}} \right.`

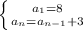
Explanation:

The given rule is

`a_(n)=3n+5`

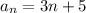
If we substitute
`n=1, n=2, n=3, n=4,..`

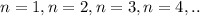
The sequence would be

`a_(1)=3(1)+5=3+5=8\\a_(2)=3(2)+5=6+5=11\\a_(3)=3(3)+5=9+5=14\\a_(4)=3(4)+5=12+5=17`

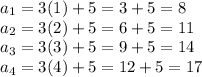
As you can observe, the arithmetic sequence has a difference of 3, that is, adding 3 units to one term, we obtain the next one. Now, we can use this rule to right a recursive rule.

First, we have to write the first term

`a_(1)= 8`

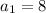
Then, we write the patter to obtain the next terms, which is adding 3 units, so

`a_(n)=a_(n-1)+3`

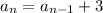
Therefore, the recursive rule for
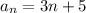`a_(n)=3n+5` is

`\left \{ {{a_(1) =8} \atop {a_(n) =a_(n-1) +3}} \right.`