Question

Earth's neighboring galaxy, the Andromeda Galaxy, is a distance of 2.54×10^7 light-years from Earth. If the lifetime of a human is taken to be 70.0 years, a spaceship would need to achieve some minimum speed ????minvmin to deliver a living human being to this galaxy. How close to the speed of light would this minimum speed be?

Answer 1

0.9999986*c

Step-by-step explanation:

The ship would travel 2.54*10^7 light years, which means that at a speed close to the speed of light the trip would take 2.54*10^7 years from the point of view of an observer on Earth. However from the point of view of a passenger of that ship it will take only 70 years if the speed is close enough to the speed of light.

`\Delta t = \Delta t' * \sqrt{1 - ((v)/(c))^2}`

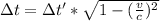
Where

Δt is the travel time as seen by a passenger

Δt' is the travel time as seen by someone on Earth

v is the speed of the ship

c is the speed of light in vacuum

We can replace the fraction v/c with x

`\Delta t = \Delta t' * √(1 - x^2)`

`√(1 - x^2) = (\Delta t)/(\Delta t')`

`1 - x^2 = ((\Delta t)/(\Delta t'))^2`

`x^2 = 1 - ((\Delta t)/(\Delta t'))^2`

`x = \sqrt{1 - ((\Delta t)/(\Delta t'))^2}`

`x = \sqrt{1 - ((70)/(2.54*10^7))^2} = 0.9999986`

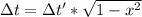
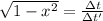
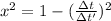
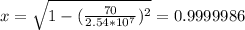
It would need to travel at 0.9999986*c