Answer:
Epx= - 21.4N/C
Epy= 19.84N/C
Step-by-step explanation:
Electric field theory
The electric field at a point P due to a point charge is calculated as follows:
E= k*q/r²
E= Electric field in N/C
q = charge in Newtons (N)
k= electric constant in N*m²/C²
r= distance from load q to point P in meters (m)
Equivalences
1nC= 10⁻⁹C
known data
q₁=-2.9nC=-2.9 *10⁻⁹C
q₂=5nC=5 *10⁻⁹C
r₁=0.840m
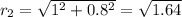
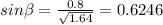
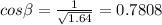
Calculation of the electric field at point P due to q1
Ep₁x=0

Calculation of the electric field at point P due to q2
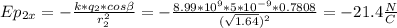
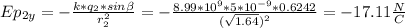
Calculation of the electric field at point P(0,0) due to q1 and q2
Epx= Ep₁x+ Ep₂x==0 - 21.4N/C =- 21.4N/C
Epy= Ep₁y+ Ep₂y=36.95 N/C-17.11N =19.84N/C