Answer:
(A). The magnetic field is zero at 0.8 cm.
(B). The magnetic field is zero at 5.56 cm.
Step-by-step explanation:
Given that,
Current in first wire I = 6.0 A
Current in second wire = 2.6 A
Distance
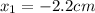
Distance
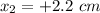
(A). We need to calculate the magnetic field
If the currents are in the same direction
The magnetic field is in both wires
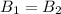
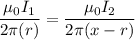
Put the value into the formula
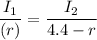
Put the value into the formula
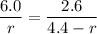
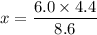
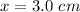
The point where the magnetic field is zero

The magnetic field is zero at 0.8 cm.
(B). We need to calculate the point where the magnetic field zero
If the currents are in the opposite direction
The magnetic field is in both wires
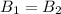
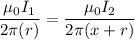
Put the value into the formula
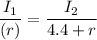
Put the value into the formula
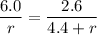
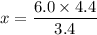
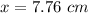
The point where the magnetic field is zero
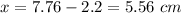
The magnetic field is zero at 5.56 cm.
Hence, This is the required solution.