Answer: The correct answer is: " 4 " .
__________________________________________
Explanation:
__________________________________________
We are given:
" log₃ 81 " ;
Note: " logₐ xⁿ = n logₐ x " ;
So: a = 3 ;
xⁿ = ? ; ↔
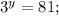
Solve for "y" ;
3² = 3 * 3 = 9 ;
3³ = 3 * 3 * 3 = (3 * 3) * 3 = 9 * 3 = 27 ;
3⁴ = 3 * 3 * 3 * 3 = (3 * 3) * 3 * 3 = 9 * 3 * 3 = (9 * 3) * 3 = 27 * 3 = 81 ;
→ 3⁴ = 81 .
__________________________________________
" log₃ 81 " ;
Note: " logₐ xⁿ = n logₐ x " ;
So: a = 3 ; x = 3 ; and n = 4 ;
Since: Given: " log₃ 81 " ;
→ log₃ 81 ; ↔ 81 = xⁿ = 3⁴ ;
______________________________________________
→ log₃ 81 = log₃ 3⁴ ; = n logₐ x ;
→ n logₐ x = ? ; Substitute: "a = 3 " ; "x = 3" ; "n = 4" ;
→ 4 log₃ 3 = ? ;
= 4 * log₃ 3 ;
→ log₃ 3 = ? ; →
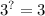 ; ↔ 3¹ = 3 ;
; ↔ 3¹ = 3 ;
↔ log₃ 3 = 1 .
→ 4 * log₃ 3 = 4 * 1 = 4.
__________________________________________
The answer is: " 4 " .
__________________________________________