Question

To practice Problem-Solving Strategy 21.1 Coulomb's Law. Three charged particles are placed at each of three corners of an equilateral triangle whose sides are of length 4.0 cm . Two of the particles have a negative charge: q1 = -7.8 nC and q2 = -15.6 nC . The remaining particle has a positive charge, q3 = 8.0 nC . What is the net electric force acting on particle 3 due to particle 1 and particle 2?

Answer 1

The force felt by charge 3 is F=(-5.6*10⁻⁶,3.36⁻⁵)N

Step-by-step explanation:

As the superposition principle applies to static charges, we can find the net electric force as the sum of the two forces felt by q3.

Looking at the drawing and knowing that they form an equilateral triangle of lenght 4 we can conclude that each internal angle is 60°.

So, the positions in our coordinate system are:

`r_1=(0,0)\\r_2=(4\ cos(60\°),4\ sin(60\°))\\r_3=(4,0)\\`

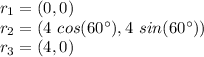
Now using Coulomb's force:

`F_(ij)=(-kq_iq_j)/(d^2)(\vv{r}_j-\vv{r}_i)`

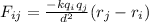
Where d=4, q1 = -7.8*10⁻⁹C, q2 = -15.6 *10⁻⁹C, q3 = 8.0 *10⁻⁹C, k=8.98*10⁹, e0=8.8*10¹⁰:

Replacing we get 2 equations:

`F_(13)=(-kq_1q_3)/(d^2)(\vv{r}_1-\vv{r}_3)=(-kq_1q_2)/(d^2)(-0.04\ cos(60\°),-0.04\ sin(60\°))\\\\</p><p>F_(23)=(-kq_2q_3)/(d^2)(\vv{r}_1-\vv{r}_3)=(-kq_1q_2)/(d^2)(0.04-0.04\ cos(60\°),-0.04\ sin(60\°))\\`

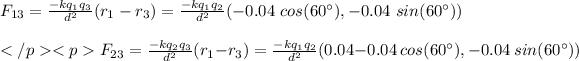
To work with the sam

F=∑F_i=3.5*10⁻⁴(0.023,0.032)+7*10⁻⁴(-0.016,0.032)=

=((3.5*10⁻⁴-7*10⁻⁴)*0.016,(3.5*10⁻⁴+7*10⁻⁴)*0.032)=

F=(-5.6*10⁻⁶,3.36⁻⁵)N