Question

If the concentration of acetic acid is 0.10 M, what is the pH of the resulting solution?

a)-2.89

b)0.10

c)7.00

d)2.89

Answer 1

Option D) 2.89.

Step-by-step explanation:

Look up the acid dissociation constant of acetic acid:

`K_(\rm a) \approx \rm 1.75* 10^(-5)`

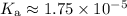
(CRC Handbook of Chemistry and Physics, 84th Edition (2004).)

Acetic acid partially dissociate to produce acetate ions and hydrogen ions:

`\rm CH_3COOH \rightleftharpoons CH_3COO^(-) + H^(+)`.

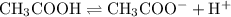Let the final concentration of
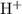`\rm H^(+)` in the solution be
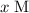`x\; \rm M`. The concentration of acetic acid would have dropped by
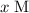`x\; \rm M` and the concentration of acetate ions would have increased by
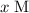`x\; \rm M`. The initial concentration of
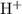`\rm H^(+)` in pure water is
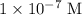`1* 10^(-7)\;\rm M` and will barely influence the outcome.

Construct a RICE table for this reaction: (all values here are in
`M`, which stands for concentrations in moles per liter.)

`\begin{array}c\textbf{R}& \mathrm{CH_3COOH} & \rightleftharpoons & \mathrm{CH_3COO^(-)} & + & \mathrm{H^(+)}\\\textbf{I} & 0.10\\ \textbf{C} & -x & & +x & & +x \\\textbf{E} & 0.10 - x & & x & & x \end{array}`.

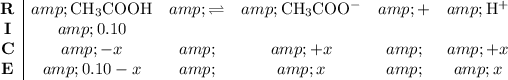At equilibrium:

• 
  `[\mathrm{CH_3COOH}] = (0.10 - x) \; \rm M`;
• 
  `[\mathrm{CH_3COO^(-)}] = x\; \rm M`;
• 
  `[\mathrm{H^(+)}] = x\; \rm M`.

By the definition of the acid dissociation constant,
`K_(\rm a)`:

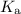`\displaystyle K_(\rm a)(\mathrm{CH_3COOH}) = \frac{[\mathrm{CH_3COO^(-)}]\cdot [\mathrm{H^(+)}]}{[\mathrm{CH_3COOH}]}`.

That is:

`\displaystyle (x^(2))/(0.10 - x) = \rm 1.75* 10^(-5)`.

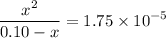Rearrange and solve for
`x`:

`x^(2) + 1.75* 10^(-5) ~x - 1.75 * 10^(-6) = 0`.

`\displaystyle x = \frac{-1.75* 10^(-5) \pm \sqrt{{\left(1.75* 10^(-5)\right)^(2)}- 4* \left(-1.75* 10^(-6)\right)}}{2}`.

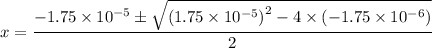There might be more than one solution to this equation. However, keep in mind that all concentration should be positive (at least non-negative.) The only possible value of
`x` will thus be approximately
`0.00131`.

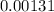In other words, at equilibrium
`[\mathrm{H^(+)}] \approx 0.00131 \; \rm M`. By the definition of pH,

`\begin{aligned} \rm pH &= -\log_(10){[\mathrm{H^(+)]}\\&= - log_10(0.00131) \\&\approx 2.9\end{aligned}`.

Note that depending on the
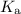`K_(\rm a)` value, the final result might slightly vary.