Question

You attach a 3.10 kg weight to a horizontal spring that is fixed at one end. You pull the weight until the spring is stretched by 0.100 m and release it from rest. Assume the weight slides on a horizontal surface with negligible friction. The weight reaches a speed of zero again 0.400 s after release (for the first time after release). What is the maximum speed of the weight (in m/s)? m/s

Answer 1

0.785 m/s

Step-by-step explanation:

Hi!

To solve this problem we will use the equation of motion of the harmonic oscillator, i.e.

`x(t) = A cos(\omega t )+B sin(\omega t)` - (1)

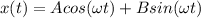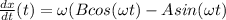`(dx)/(dt)(t) = \omega (B cos(\omega t )- A sin(\omega t)` - (1)

The problem say us that the spring is released from rest when the spring is stretched by 0.100 m, this condition is given as:

`x(0) = 0.100`

`(dx)/(dt)(0) = 0`

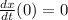
Since cos(0)=1 and sin(0) = 0:

`x(0)=A`

`(dx)/(dt)(0) = -B\omega`

We get

`A =0.100\\B = 0`

Now it say that after 0.4s the weigth reaches zero speed. This will happen when the sping shrinks by 0.100. This condition is written as:

`x(0.4) = - 0.100`

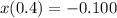
Since

`x(t) = 0.100 cos(\omega t)\\ -0.100=x(0.4)=0.100cos(\omega 0.4)`

This is the same as:

`-1 = cos(0.4\omega)`

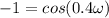
We know that cosine equals to -1 when its argument is equal to:

(2n+1)π

With n an integer

The first time should happen when n=0

Therefore:

π = 0.4ω

or

ω = π/0.4 -- (2)

Now, the maximum speed will be reached when the potential energy is zero, i.e. when the sping is not stretched, that is when x = 0

With this info we will know at what time it happens:

`0 = x(t) = 0.100cos(\omega t)`

The first time that the cosine is equal to zero is when its argument is equal to π/2

i.e.

`t_(maxV)=\pi /(2\omega)`

And the velocity at that time is:

`(dx)/(dt)(t_(maxV) ) =- 0.100\omega sin(\omega t_(maxV))\\(dx)/(dt)(t_(maxV) ) =- 0.100\omega sin(\pi/2)\\`

But sin(π/2) = 1.

Therefore, using eq(2):

`(dx)/(dt)(t_(maxV) ) = 0.100*\omega = 0.100(\pi)/(0.400) = \pi/4`

And so:

`V_(max) = \pi / 4 =0.785`