Question

Three equal charges of magnitude 'e' are located at the vertices of an equilateral triangle of side 1m. Where should you place a charge of 2e' so that the '2e' does not experience any force?

Answer 1

At centroid

Step-by-step explanation:

In the given equilateral triangle ABC with side of 1 m. The three equal charges e,e,e are placed at the A,B and C.

And the fourth charge 2e is put at point O which is called centroid.

Now we can calculate the distance AD by applying pythagorean theorem as,

`AD^(2)=AB^(2)+BD^(2)`

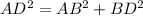
Put the values and get.

`AD^(2)=1^(2)+((1)/(2) )^(2)\\AD=\sqrt{(3)/(4) } \\AD=(√(3))/(2)`

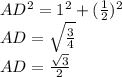
Now calculate AO as,

`AO=(2)/(3)* (√(3) )/(2)\\AO=(1)/(√(3) )`

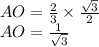
And the sides BO=CO=AO.

Now Force can be calculated as

`F_(1)=(2ke^(2) )/((1)/(√(3) ) ^(2) )\\F_(1)=6ke^(2)`

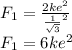
And similarly,

`F_(2)=F_(3)=6ke^(2)`

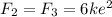
Now we can calculate resultant of
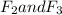`F_(2)andF_(3)` in upward direction. as,

`F_(net)=\sqrt{F_(2)^(2)+F_(3)^(2)+2F_(2)F_(3)cos120  } \\F_(net)=\sqrt{F_(2)^(2)+F_(2)^(2)+2F_(2)F_(2)(-(1)/(2))}\\F_(net)=6ke^(2)`

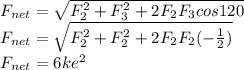
Therefore the resultant force on centroid O.

`F=F_(1)-F_(net)\\F=6ke^(2)-6ke^(2)\\F=0`

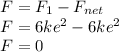
Therefore the fourth charge 2e should be placed on centroid so that it experience zero force.