Answer:
3(x-5)(x-2)
Explanation:
First you can take 3 as a common factor:
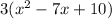
Then you can take two ways:
Use the resolver ecuation to get the roots, or think in two numbers that the sum is -7 and the product is 10.
The only two integers that we can choice are -5 and -2
(-5)*(-2)=10
-5+(-2)=-7
Then you can write the ecuation as a product of its roots:
3 * (x-5) * ( x-2)
And its the same expresion as:
3x^2-21x+30
To be sure you are doing well, solve the product of your solution and you will have the same expresion.