Question

Gaussian surface in the shape of a right circular cylinder with end caps has a radius of 12.0 cm and a length of 80.0 cm. Through one end there is an inward magnetic flux of 25.0 mWb. At the other end there is a uniform magnetic field of 1.60 mT, normal to the surface and directed outward. What are the (a) magnitude and (b) direction (inward or outward) of the net magnetic flux through the curved surface?

Answer 1

(a). The magnitude of the flux is 47.3 μWb.

(b). If the sign of magnetic flux is negative then the magnetic flux will be inward.

Step-by-step explanation:

Given that,

Radius = 12.0 cm

Length = 80.0 cm

Magnetic flux = 25.0 mWb

Magnetic field = 1.60 mT

(a). We need to calculate the magnitude the net magnetic flux through the curved surface

Using formula of magnetic flux

The total net magnetic flux is equal to the sum of the magnetic flux the first end add magnetic flux through the second end add magnetic flux the third surface

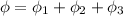`\phi=\phi_(1)+\phi_(2)+\phi_(3)`....(I)

According to Gauss's law

`\int{\vec{B}\cdot\vec{dA}}=0`

Here,
`\phi_(1)=-25\ mWb`

Negative sign show the inward flux

Now,
`\phi_(2)=\vec{B}\cdot\vec{A}`

`\phi_(2)=\pi r^2B`

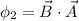
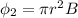
Put the value into the formula

`\phi_(2)=\pi*(12.0*10^(-2))^2*1.60*10^(-3)`

`\phi_(2)=0.0723*10^(-3)\ Wb`

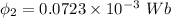
Here, The direction of magnetic field is outward.

We need to calculate the third flux

`\phi_(3)=-\phi_(1)-\phi_(2)`

`\phi_(3)=-25.0\ mu Wb+72.3\ \mu Wb`

`\phi_(3)=-47.3\ \mu Wb`

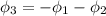
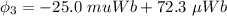
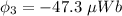
The magnitude of the flux is 47.3 μWb.

(b). If the sign of magnetic flux is negative then the magnetic flux will be inward.

Hence, This is the required solution.