Question

A 0.12 kg block on a horizontal frictionless surface is attached to a spring whose force constant is 330 N/m. The block is pulled from its equilibrium position at x = 0 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the x-axis (horizontal). The velocity of the block at time t = 0.7 s is closest to: A) -4.9 m/s B) 4.9 m/s C) 3.5 m/s D) -3.5 m/s E) zero

Answer 1

The velocity of the block is 3.5 m/s.

(C) is correct option.

Step-by-step explanation:

Given that,

Mass of block = 0.12 kg

Force constant = 330 N/m

Time = 0.7 s

We need to calculate the angular frequency

Using formula of angular frequency

`\omega=\sqrt{(k)/(m)}`

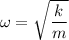
Put the value into the formula

`\omega=\sqrt{(330)/(0.12)}`

`\omega=5√(110)\ Hz`

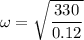
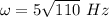
We need to calculate the velocity of the block

Using simple harmonic motion

`x=A\sin(\omega t+\phi)`

`x=A\cos\omega t`

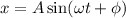
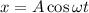
On differentiating with respect to t

`(dx)/(dt)=-A\omega\sin\omega t`

`v=-A\omega\sin\omega t`

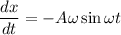
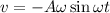
Put the value into the formula

`v=-0.080*5√(110)\sin(5√(110)*0.7)`

`v=3.5\ m/s`

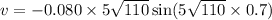
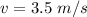
Hence, The velocity of the block is 3.5 m/s.