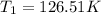Question

A sample of helium has a volume of 12.7 m3. The temperature is raised to 323 K at which time the gas occupies 32.5 m3? Assume pressure is constant at 3 atm. What was the original temperature of the gas?

Answer 1

126.22

Step-by-step explanation:

Answer for Educere/ Founder's Education

Answer 2

Answer: The original temperature was

`T_(1)=126.51K`

Step-by-step explanation:

Let's put the information in mathematical form:

`V_(1)=12.7m^(3)`

`T_(1)=?`

`V_(2)=32.5m^(3)`

`T_(2)=323K`

`P_(1)=P_(2)=3atm`

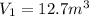
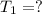
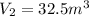
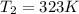
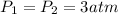
If we consider the helium as an ideal gas, we can use the Ideal Gas Law:

`PV=nRT`

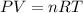
were R is the gas constant. And n is the number of moles (which we don't know yet)

From this, taking
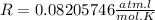`R=0.08205746(atm.l)/(mol.K)`, we have:

`n=(P_(2)V_(2))/(RT_(2))`

⇒
`n=3.67mol`

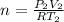
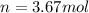
Now:

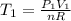
`T_(1)=(P_(1)V_(1))/(nR)`

⇒
`T_(1)=126.51K`