Question

The current in a circuit element is i(t) = 3(1 - e-2t) A when t ≥ 0 and i(t) = 0 when t < 0. The total charge that has entered the circuit element for t ≥ 0 can be represented as q left-parenthesis t right-parenthesis equals Upper A ⁢ plus Upper B t plus Upper C e Superscript negative a t coulomb, where A, B, C and a are real constants. Determine the values of A, B, C and a.

Answer 1

A=-3/2

B=3

c=3/2

a=-2

Explanation:

Knowing that for
`t>0`
`i(t)=2\left(1-e^(-2t)\right) A`,
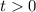
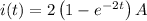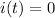`i(t)=0` when t<0 and using the definition of charge

`q(t)=\int_(-\infty)^0i(t')dt'+\int_0^t i(t')dt'=0+\int_0^t i(t')dt'`

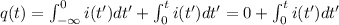
The first term corresponds to q(0), the charge accumulated before t=0, in this case it luckily gives zero so we don't have to worry about it.

Let's proceed and integrate
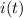`i(t)` then when t>0

`i(t)=3\int_0^t \left[ \int_0^tdt'-\inte_0^t e^(-2t')dt' \right]dt'=3\left[ t+(1)/(2)\left( e^(-2t)-1 \right) \right]=3t+(3)/(2)e^(-2t)-(3)/(2)\,\, C`

It is clear that:

A=-3/2

B=3

c=3/2

a=-2