Question

Suppose ten students in a class are to be grouped into teams. (a) If each team has two students, how many ways are there to form teams? (The ordering of students within teams does not matter, and the ordering of the teams does not matter.) (b) If each team has either two or three students, how many ways are there to form teams?

Answer 1

(a) There are 113,400 ways

(b) There are 138,600 ways

Explanation:

The number of ways to from k groups of n1, n2, ... and nk elements from a group of n elements is calculated using the following equation:

`(n!)/(n1!*n2!*...*nk!)`

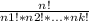
Where n is equal to:

n=n1+n2+...+nk

If each team has two students, we can form 5 groups with 2 students each one. Then, k is equal to 5, n is equal to 10 and n1, n2, n3, n4 and n5 are equal to 2. So the number of ways to form teams are:

`(10!)/(2!*2!*2!*2!*2!)=113,400`

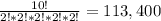
For part b, we can form 5 groups with 2 students or 2 groups with 2 students and 2 groups with 3 students. We already know that for the first case there are 113,400 ways to form group, so we need to calculate the number of ways for the second case as:

Replacing k by 4, n by 10, n1 and n2 by 2 and n3 and n4 by 3, we get:

`(10!)/(2!*2!*3!*3!)=25,200`

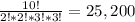
So, If each team has either two or three students, The number of ways form teams are:

113,400 + 25,200 = 138,600