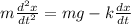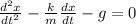Answer:
The DE will be
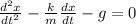
Step-by-step explanation:
We have to find differential equation under the influence of gravity and experiencing a resistive force
Let an object of mass m falling under the influence of gravity
So the force experience under gravity

Le the a resistive force of magnitude kv opposes this gravity force, here k is constant and v is velocity.
So net force
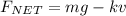 -----eqn 1
-----eqn 1
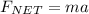
So
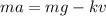
We know that velocity is rate of change of position so
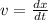 , and acceleration is rate of change of velocity so
, and acceleration is rate of change of velocity so
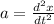
Putting all these value in eqn 1