Answer:
(a) The power input to the compressor:
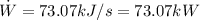
(b) The volume flow rate of the refrigerant at the compressor inlet:
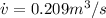
Step-by-step explanation:
(a)
We need to check the values of enthalpy (as we have an open system) for both states, being the inlet, state 1 and the outlet, state 2. We will know these values by checking the vapor charts of R134a, I used the ones found in Thermodynamics of Cengel, 7th edition.
Then, our values are:
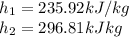
Now we proceed to know the work with the following expression:
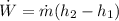
Now we replace values and our result is:
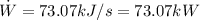
(b)
To know the volume rate at the compressor inlet, we need to know the specific volume in that phase, as we have that is saturated and at -24°C, we can read our table:
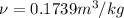
With our specific volume and the mass rate, we can calculate the volume rate: