Ix identical square pyramids can fill the same volume as a cube with the same base. If the height of the cube is h units, what is true about the height of each pyramid? a.The he…

Question

asked Oct 21, 2020 132k views

1 Answer

Jcpennypincher · Answer 1 · 2020-10-25T02:52:08+0000

Answer:

height of each pyramid must be 3h units

Step-by-step explanation:

As we know that the volume of the cube is same as that of volume of square pyramid

so we have volume of the cube is given as

V = h^3

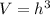
now if the base area of pyramid and the cube is same

so we will have

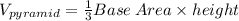
$V_(pyramid) = (1)/(3) Base\: Area * height$

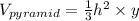
V_(pyramid) = (1)/(3) h^2 * y

now since both have same volume

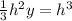
(1)/(3)h^2 y = h^3

y = 3h

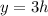
height of each pyramid must be 3h units