Question

ou drive on Interstate 10 from San Antonio to Houston, half the time at 77 km/h and the other half at 119 km/h. On the way back you travel half the distance at 77 km/h and the other half at 119 km/h. What is your average speed (a) from San Antonio to Houston, (b) from Houston back to San Antonio, and (c) for the entire trip

Answer 1

Part a)98 km/h

Part b) 93.5 km/h

Part c) 95.7 km/h

Step-by-step explanation:

A) For the trip from Antonio to Houston we have

Let the total time in which the trip is completed be 't'

Thus the distance covered with a speed of 77 km/h equals
`77* (t)/(2)`

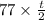
Similarly the distance covered with a speed of 119 km/h equals
`119* (t)/(2)`

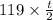
Now by definition of average speed we have

Average Speed =
`(Distance)/(time)`

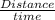
Applying values we get

Average Speed for trip 1 =
`(77* (t)/(2)+119* (t)/(2))/(t)`

Thus average speed equals
`(77+119)/(2)=98km/h`

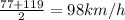
B)For the trip from Houston Antonio to we have

Let the total distance of the trip be 'd'

Time required to complete half the distance at a speed of 77 km/h equals
`t_(1)=(0.5d)/(77)`

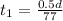
Time required to complete remaining half the distance at a speed of 119 km/h equals
`t_(1)=(0.5d)/(119)`

Now by definition of average speed we have

Average Speed =
`(Distance)/(time)`

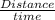
Applying values we get

Average Speed for trip 1 =
`(d)/((0.5d)/(77)+(0.5d)/(119))`

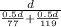
Thus average speed equals
`(1)/((0.5)/(77)+(0.5)/(119))=93.5km/h`

C) For the entire trip we have

Average Speed =
`(Distance)/(time)`

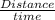
Applying values we get

Average Speed for both the trips =
`(2d)/((2d)/(77+119)+(0.5d)/(77)+(0.5d)/(119))`

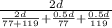
Thus average speed for both the trips equals 95.7 km/h