Answer:
t = 1.48 s
Step-by-step explanation:
As we know that length of the Boeing plane is
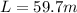
width of the intersection is given as

now we know that deceleration of the plane is given as
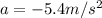
Also the final speed of the plane while it clears the intersection is given as

now we have
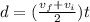
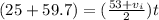
also we know that
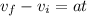
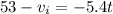
now we have
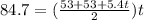
by solving above equation we have
