Answer:
The angular frequency of oscillation of the mass is 11 rad/s.
Step-by-step explanation:
Given that,
Charge = 2μC
Radius R₁= 8 cm
Radius R₂ = 16 cm
Angular frequency = 22 rad/s
We need to calculate the angular frequency of oscillation of the mass
The electric field produced along x axis
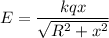
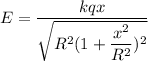
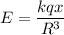
The force on the mass is
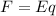
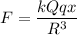 ....(I)
....(I)
For,x<<R
Now, using centripetal force
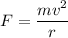
Put the value of F in equation (I)

We know that,
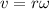
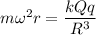
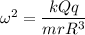
For, r<<R
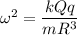
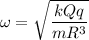
Here,
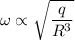
The ratio of angular frequency
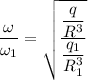
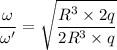

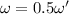
Put the value of
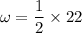
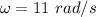
Hence, The angular frequency of oscillation of the mass is 11 rad/s.