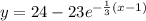Answer:
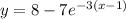
Explanation:
Assuming that the equation is
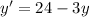 with initial condition
with initial condition
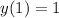 . We have,
. We have,
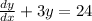 , hence we can say that
, hence we can say that
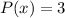 and
and
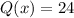 in the general form of the first order linear differential equation:
in the general form of the first order linear differential equation:
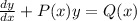
The integrating factor is given by:
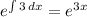 . Thus, multiplying the entire equation by the integrating factor:
. Thus, multiplying the entire equation by the integrating factor:
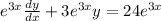 . This means that:
. This means that:
![(d[e^(3x)y])/(dx) = 24e^(3x)](https://img.qammunity.org/2020/formulas/mathematics/college/ievjets0lj901hbae65faqftpcibm0bz38.png)
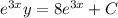 then
then
 . Applying the initial condition:
. Applying the initial condition:
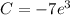 and therefore,
and therefore,
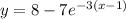
Assuming that the equation is
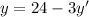 with initial condition
with initial condition
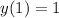 . We have,
. We have,
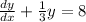 , hence we can say that
, hence we can say that
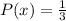 and
and
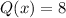 in the general form of the first order linear differential equation:
in the general form of the first order linear differential equation:
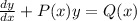
The integrating factor is given by:
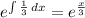 . Thus, multiplying the entire equation by the integrating factor:
. Thus, multiplying the entire equation by the integrating factor:
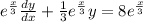 . This means that:
. This means that:
![\frac{d[e^{(x)/(3)}y]}{dx} = 8e^{(x)/(3)}](https://img.qammunity.org/2020/formulas/mathematics/college/hl8d7c8jp1a5elthqrbl6890lwz7abaqeh.png)
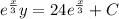 then
then
 . Applying the initial condition:
. Applying the initial condition:
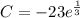 and therefore,
and therefore,