Question

A pipe, 4.5 cm in diameter and 1×104 cm in length, transports superheated vapor at a rate of 1.08× 106 grams/h. The pipe, which is located in a power plant at 300 K, has a uniform surface temperature of 370 K. If the temperature drop between the inlet and exit of the pipe is 35 K, determine the heat transfer coefficient as a result of convection between the pipe surface and the surroundings. Assume, the specific heat of the vapor is 2190 J/kg.K. (20 points)

Answer 1

h = 23.237 W/m2 K

Step-by-step explanation:

given data:

flow rate = 1.08*10^6 gm/h = 0.3 kg/s

D = 4.5 cm = 0.045 m

L = 10^4 cm = 100 m

surface temperature = 370 K

`\Delta T = 35K`

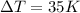
Surface heat of vapor = 2190 J/kg.k

From energy conservation principle we have

heat transfer btwn surface and air = heat loss due to flow and temp. drop

where

heat transfer btwn surface and air is due to convection

`Q _(convection) = hA_s (T_S - T_∞)`

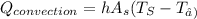
WHERE

`T_S = 370 K`

`T_∞ = 300 K`

`Heat\ loss  = Q_(loss) = \dot m Cp \Delta T`

`\dot m = 0.3 kg/s`

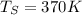
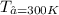
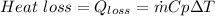
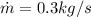
from both above equation we have

`Q_(convection) = Q_(loss)`

`hA_s (T_S - T_∞) = \dot m Cp \Delta T`

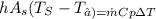
putting all value to get heat transefer coefficient

`h = (\dot m Cp \Delta T)/(A_S((T_S - T_∞))`

`h = (0.3*2190*35)/(14.137*(370-300))`

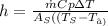
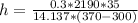
h = 23.237 W/m2 K