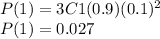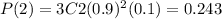Question

In a semiconductor manufacturing process, three wafers from a lot are tested. Each wafer is classified as pass or fail. Assume that the probability that a wafer passes the test is 0.9 and that wafers are independent. Determine the probability mass function of the number of wafers from a lot that pass the test. Round your answers to three decimal places

Answer 1

Explanation:

Given that in a semiconductor manufacturing process, three wafers from a lot are tested. We find that each wafer in independent of the other, and there are only two outcomes.

Hence X no of wafers that pass the test from the three selected is binomial with n = 3 and p = 0.9 q =0.1

Probability mass function would be

`P(0) =0.1^3 =0.001`

`P(1) = 3C1(0.9)(0.1)^2\\P(1) = 0.027`

`P(2) = 3C2(0.9)^2(0.1) = 0.243`

`P(3) = 0.9^3 = 0.729`