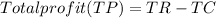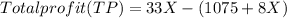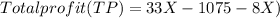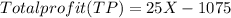Question

Phil makes and sells rugs at his roadside stand. His monthly fixed cost for owning the stand is $1075. If he makes and sells 19 rugs, his total costs are $1227 and he brings in $627 in revenue. Find Phil's monthly cost, revenue, and profit functions (assuming they are linear). Let x be the number of rugs made and sold each month

Answer 1

Monthly cost (Total cost):

`Total cost (TC)=1075 + 8X`

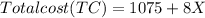
Monthly revenue (Total revenue):

`Total revenue(TR)=33X`

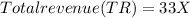
Monthly profit (Total profit):

`Total profit (TP) = 25X - 1075`

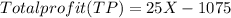
Step-by-step explanation:

Ok, firts we organice our information:

Fixed cost (FC) = 1075

Rugs produced (X) = 19

Total cost if the production is 19 rugs = 1227

Total Revenue if the production is 19 rugs = 627

We can find the Total cost function from the information provided:

`Total cost=Fixed cost(FC) + Variable cost(VC)`

`1227=1075 + VC(X)`

`1227=1075 + VC(19)`

`VC(19)=1227- 1075`

`VC=(152)/(19)`

`VC=8`

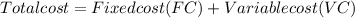
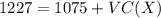
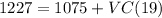
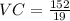
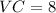
We now replace in the Total cost function:

`Total cost  (TC)=1075 + 8X`

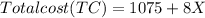
We con now find the total revenue:

`Total revenue (TR) = Price(P)*Quantity(X)`

`627=P*19`

`P=(627)/(19)`

`P=33`

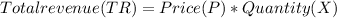
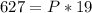
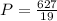
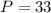
Now we replace in the Total revenue function:

`Total revenue(TR)=33X`

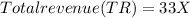
Having the TC and TR function we find the Profit function:

`Total profit (TP) = TR - TC`

`Total profit (TP) = 33X - (1075 + 8X)`

`Total profit (TP) = 33X - 1075 - 8X)`

`Total profit (TP) = 25X - 1075`