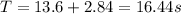Question

slader Question: A Model Rocket Is Launched Straight Upward With An Initial Speed Of 50m/s. Iit Accelerates With A Constant Upward Acceleration Of 2.0 M/s^2 Until Its Engine Stops At An Altitude Of 150m. Calculate The Maximum Heigght Reached By The Rocket And How Long The Rocket Is In The Air.

Answer 1

Maximum height reached by the rocket is

`y_(max) = 308 m`

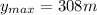
total time of the motion of rocket is given as

`T = 16.44 s`

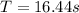
Step-by-step explanation:

Initial speed of the rocket is given as

`v_i = 50 m/s`

acceleration of the rocket is given as

`a = 2 m/s^2`

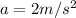
engine stops at height h = 150 m

so the final speed of the rocket at this height is given as

`v_f^2 - v_i^2 = 2 a d`

`v_f^2 - 50^2 = 2(2)(150)`

`v_f = 55.68 m/s`

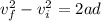
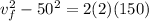
so maximum height reached by the rocket is given as the height where its final speed becomes zero

so we will have

`v_f^2 - v_i^2 = 2 a d`

`0 - 55.68^2 = 2(-9.81)(y - 150)`

`y_(max) = 308 m`

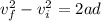
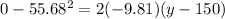
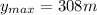
Now the total time of the motion of rocket is given as

1) time to reach the height of 150 m

`v_f - v_i = at`

`55.68 - 50 = 2 t`

`t_1 = 2.84 s`

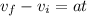
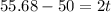
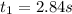
2) time to reach ground from this height

`\Delta y = v_y t + (1)/(2)gt^2`

`-150 = 55.68 t - (1)/(2)(9.81) t^2`

`t_2 = 13.6 s`

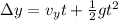
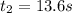
so total time of the motion of rocket is given as

`T = 13.6 + 2.84 = 16.44 s`