Answer: 1) b. 20° 2) a. 4 3) a. 4 4) c. 34°
Explanation:
1) Since TV bisects ∠STU, then ∠UTV = ∠STV and 2(∠UTV) = ∠STV
∠UTV = ∠STV
x + 2 =
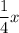 +8
+8
4x + 8 = x + 32 multiplied by 4 to clear the denominator
3x + 8 = 32 subtracted x from both sides
3x = 24 subtracted 8 from both sides
x = 8 divided both sides by 3
2(∠UTV) = ∠STV
2(x + 2) = ∠STV
2(8 + 2) = ∠STV
2(10) = ∠STV
20 = ∠STV
*******************************************************************************
2) Since SR bisects ST, then 2(SR) = ST
2(SR) = ST
2(3x + 3) = 30
3x + 3 = 15 divided both sides by 2
3x = 12 subtracted 3 from both sides
x = 4 divided both sides by 3
*********************************************************************************
3) Since K is the midpoint of JL, then 2(JK) = JL
2(JK) = JL
2(7) = 4x - 2
14 = 4x - 2 multiplied 2 and 7
16 = 4x added 2 to both sides
4 = x divided 4 from both sides
*********************************************************************************
4) Since QS is the midpoint, then 2(∠PQS) = ∠PQR
2(∠PQS) = ∠PQR
2(5y - 1) = 8y + 12
10y - 2 = 8y + 12
2y - 2 = 12 subtracted 8y from both sides
2y = 14 added 2 to both sides
y = 7 divided 2 from both sides
∠PQS = 5y - 1
= 5(7) - 1
= 35 - 1
= 34