Question

1. Calculate the pH of a 2.5M solution of NH3 (Kb = 1.8 x 10-5 ).

Answer 1

11.83

Step-by-step explanation:

Ammonia dissolves in water according to the equilibrium expression:

`NH_(3) _((g)) + H_(2)O_((l)) = NH4^(+) _((aq)) + OH^(-)_((aq))`

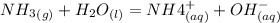
At equilibrium, a small amount dissociates, therefore:

kb = 1.8 * 10⁻⁵

pH = 2.5

the dissociation costant is given by the equilibrium amounts. This is given as:

NH₃ = (2.5 - x)

NH₄ = x

OH = x

The constant, Kb is given by:

`(x^(2) )/((2.5 -x)) = 1.8 * 10^(-5)`

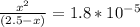
but x is so small that is equal to 0

Hence:

`OH^(-) = \sqrt{(1.8*10^(-5)*(2.5) }`

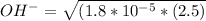
= 0.006708

pOH = -log (OH)

= -log (0.006708)

= 2.173

pH = 14 - pOH

= 14 - 2.173

= 11.826

= 11.83

Answer 2

11.83.

Step-by-step explanation:

∵ pOH = - log[OH⁻]

∵ [OH⁻] = √(Kb.C),

Kb = 1.8 x 10⁻⁵, C = 2.5 M.

∴ [OH⁻] = √(Kb.C) = √(1.8 x 10⁻⁵)(2.5 M) = 6.71 x 10⁻³ M.

∴ pOH = - log[OH⁻] = - log(6.71 x 10⁻³ M) = 2.17.

∵ pH + pOH = 14.

∴ pH = 14 - pOH = 14 - 2.17 = 11.83.