Answer:
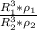
Step-by-step explanation:
The mass density of an object with uniform mass distribution its defined as
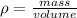 .
.
So, if we know the volume, and, we can obtain the mass of the object:
 .
.
Now, we can take the planets as spheres, of course, this is only an approximation, but good enough for us. The volume of a sphere of radius r its:
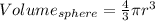
So, for our planets, the mass its given by:
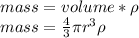 ,
,
so
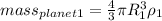
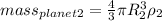
Now, we can take the ratio:
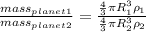
Now, we can just cancel the
![(4)/(3) \pi [\tex] that appear in both sides of our fractions, and finally obtain: </p><p>[tex](R_1^3 * \rho _1)/(R_2^3 * \rho _2)](https://img.qammunity.org/2020/formulas/physics/high-school/caicdo3h971oo9mhnp933xim0bogvxtban.png) .
.