Answer: The amount of tea ounces that sells for $ 3.25 is 36, and the amount of tea ounces that sells for $ 2.50 is 54.
Explanation:
We start by defining variables from the data provided:
a = amount of ounces of tea that sells for $ 3.25
b = amount of ounces of tea that sells for $ 2.50
c = amount of ounces of tea that sells for $ 2.80
From the problem we know that
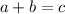 , and that
, and that
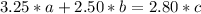 . You can propose a system of equations:
. You can propose a system of equations:
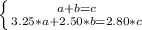
Having the fact that c = 90, we can simplify the system:
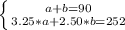
Clearing a in the first equation we get:
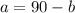
And substituting in the second equation we arrive at:

Now we can use b in the first equation to get a:
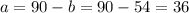
We verify that
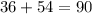 , and that
, and that
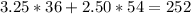 .
.