Question

Each term of a sequence, after the first term, is inversely proportional to the term preceding it, and the constant of proportionality stays the same. If the first term is 2 and the second term is 5, what is the 12th term?

Answer 1

5

Explanation:

Recall that two quantities are inversely proportional if their product is constant. Therefore, the product of every pair of consecutive terms of the sequence is the same. Since the first two terms are 2 and 5, the product of every pair of consecutive terms is 10. Therefore, the third term is 10/5=2, the fourth term is 10/2=5, and so on. We see that the n'th term is 5 for every even n, so the 12th term is 5.

Answer 2

The 12th term of the sequence is 5.

Explanation:

Inversely proportional relation:

`y\propto (1)/(x)`

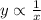
It can be written as

`y=(k)/(x)`

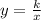
where, k is constant of proportionality.

First term is 2 and second term is 5. It is given that after first term, each term is inversely proportional to the term preceding it, and the constant of proportionality is same. It means

`a_2=(k)/(a_1)`

`5=(k)/(2)`

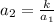
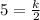
Multiply both sides by 2.

`10=k`

The constant of proportionality for given sequence is 10.

`a_3=(k)/(a_2)=(10)/(5)=2`

`a_4=(k)/(a_3)=(10)/(2)=5`

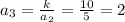
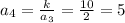
Subsequent terms will alternate between 2 and 5, with the odd terms being 2 and the even terms being 5.

12th term is an even term, so

`a_(12)=5`

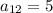
Therefore the 12th term of the sequence is 5.