Question

Under control conditions, flow through a blood vessel is 100 ml/min with a pressure gradient of 50 mm Hg. What would be the approximate flow through the vessel after increasing the vessel diameter by 100%, assuming the pressure gradient is maintained at 50 mmHg?

Answer 1

Answer: flow = 1600 ml/min

Hi!

This problem si solved using Poiseuille law, which predicts the flow φ of a viscous fluid through a tube:

`\phi = (\pi r^4)/(8\eta) (\Delta P)/(L)`

`L = length\\r = radius\\\Delta P = \text{pressure gradient}\\\eta = viscosity`

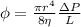
We can calculate the ratio of initial (1) and final (2) flow. As we keep the same length, and viscosity, and pressure gradient the ratio is:

`(\phi_2)/(\phi_1) = ((r_2)/(r_1) )^4`

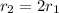`r_2 = 2r_1` (100% increase in radius)

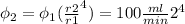`\phi_2 = \phi_1 ((r2)/(r1)^4) = 100(ml)/(min) 2^4` = 1600 ml/min