Answer:
To the right relative to the original frame.
Step-by-step explanation:
In first reference frame S,
Spatial interval of the event,
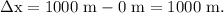
Temporal interval of the event,

In the second reference frame S', the two flashes are simultaneous, which means that the temporal interval of the event in this frame is
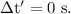
The speed of the frame S' with respect to frame S = v.
According to the Lorentz transformation,

And positive v means the velocity of the second frame S' is along the positive x-axis direction, i.e., to the right direction relative to the original frame S.