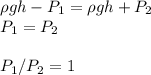Question

The pressure at the bottom of a 3-foot-deep lake several miles in diameter is P1. The pressure at the bottom of a 3-foot-deep hot tub 2 meters in diameter is P2. What relationship would P1 and P2 have?

Answer 1

P1=P2

Step-by-step explanation:

For a uniform density fluids, the pascal law say that :

`P=P_0 +\rho gh`

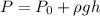
Where P is the pressure inside the fluid,
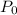`P_0` is the pressure over the fluid surface,
`\rho` is the fluid density and h is the deep.

For both cases the fluid is water, therefore the density
`\rho` is the same for both cases.

The same analysis apply for the deep h.

The equation for the lake:

`P_1=P_0 + \rho gh`

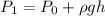
For the tub

`P_2=P_0 + \rho gh`

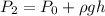
The pressure over the surface is the same for both cases, so is possible clearing Po and match the equations

`\rho gh-P_1=\rho gh+P_2  \\P_1=P_2 \\\\P_1 / P_2=1`