Question

Let n be a positive integer and define [n] to be the set of the first n positive integers. That is, [n] = {1, 2, 3, . . . , n}. We want to select two disjoint, possibly empty subsets A, B of [n]. In how many ways can we do this?

Answer 1

Answer: There are
`2^(n-1)` ways of doing this

Hi!

To solve this problem we can think in term of binary numbers. Let's start with an example:

n=5, A = {1, 2 ,3}, B = {4,5}

We can think of A as 11100, number 1 meaning "this element is in A" and number 0 meaning "this element is not in A"

And we can think of B as 00011.

Thinking like this, the empty set is 00000, and [n] =11111 (this is the case A=empty set, B=[n])

This representation is a 5 digit binary number. There are
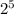`2^5` of these numbers. Each one of this is a possible selection of A and B. But there are repetitions: 11100 is the same selection as 00011. So we have to divide by two. The total number of ways of selecting A and B is the
`2^(5-1) = 2^4`.

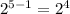This can be easily generalized to n bits.