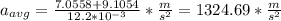Answer:
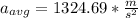
Explanation:
The average acceleration is given by:
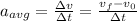
where
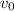 is the velocity of the ball an instant before hitting the ground and
is the velocity of the ball an instant before hitting the ground and
 an instant after.
an instant after.
we can obtain
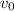 by applying the following formula:
by applying the following formula:
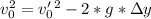
where
 since the ball falls from rest, g is the acceleration of gravity and
since the ball falls from rest, g is the acceleration of gravity and
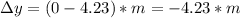
then:
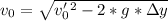
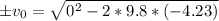
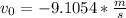 (note that here we select the negative result because of the downwards direction of the velocity)
(note that here we select the negative result because of the downwards direction of the velocity)
Similarly, we calculate
 with the formula:
with the formula:
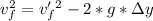
where
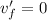 is the velocity at the maximum height, and
is the velocity at the maximum height, and
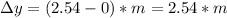
then:

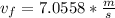
Finally the average acceleration is: