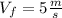Question

A pebble is released from rest at a certain height and falls freely, reaching an impact speed of 4 m/s at the floor. Next, the pebble is thrown down with an initial speed of 3 m/s from the same height. What is its speed at the floor?

Answer 1

5 m/s

Step-by-step explanation:

We can use the following formula, from kinematics, for an object travelling an distance d with constant acceleration a:

`V_f^(2) - V_i^(2) = 2 * a *d`

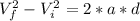
Where
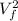`V_f^(2)` its the square of the final speed, and
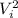`V_i^(2)` its the square of the initial speed.

For the pebble on this problem, in the release, we have an initial speed of 0 m/s, and a final speed of 4 m/s. The acceleration its constant, of course, the gravitational acceleration of the earth ( g = 9.8 m/s^2) and the distance its unknown. We can write this down:

`(4 (m)/(s))^(2) - (0 (m)/(s))^(2) = 2 * g *d`

`16 (m^(2))/(s^(2))  = 2 * g *d`

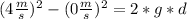
In the thrown, we got the exact same values, for acceleration and distance, but the initial speed will be 3 m/s, and the final speed its unknown.

`V_f^(2) - (3 (m)/(s))^(2) = 2 * g *d`

`V_f^(2) - 9 (m^(2))/(s^(2)) = 2 * g *d`

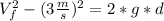
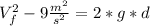
Now, we could obtain the height of the fall from our release equation, and plug it on the thrown equation. But, we could also see that the second part of this equations are the same ( 2 * g *d). So, we can write:

`V_f^(2) - 9 (m^(2))/(s^(2)) = 16 (m^(2))/(s^(2))`

`V_f^(2) = 16 (m^(2))/(s^(2)) + 9 (m^(2))/(s^(2))`

`V_f^(2) = 25 (m^(2))/(s^(2))`

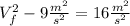
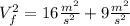
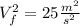
Now we can just take the root of both sides:

`V_f = 5 (m)/(s)`